-N次方怎么算？

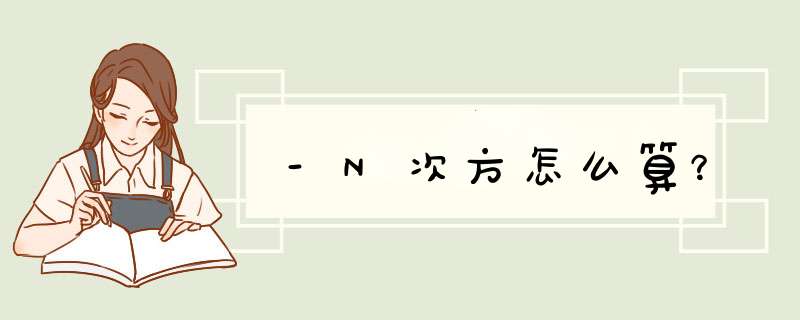
先算两次方，三次方，最多算到4次方，就可以知道n次方，严格证明需要用数学归纳法。

矩阵运算在科学计算中非常重要，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置。

扩展资料：

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵。

对称矩阵的正定性与其特征值密切相关。矩阵是正定的当且仅当其特征值都是正数。

垂直电商在初期，因为目标更具体，所以能够集中资源完成破冰，也就是更快的打开局面。

但是中期发力不足，很容易流量达到瓶颈。如果这个时候做不好转化或者独特的领先优势，那么很容易被综合电商的流量打趴下。

后期其实比综合电商好，因为综合电商体量大了，那么就会出现虹吸效应，大家都在抢流量，就只有几家赚钱，众多小店根本无法存活。

所以，很多电商都开始开辟新的路径，寻求线上线下结合。但是这时候综合电商因为体量问题，转身很难，涉及的方面很多。反而垂直电商，如果能够活到后期，是可以再度追赶上来的。那么不同垂直领域，结合方式也不一样。目前来看，文化和化妆品类的有实体优势，且贴近生活所需，实体的需求反而大于线上的需求，因此，这两个行业的转型是非常有希望的从实际效果看，暂时看不出核心优势。因为现在还是流量为王。引流成本居高不下的时候，只有用提升客单价和转化率的方法先生存下去。所以基本起家都是垂直品类，后来丰富成了综合品类。要的就是有效的客流再次利用。无论淘宝，京东，亚马逊，当当，唯品会都已经不垂直，而他们创始初期都垂直。但是，从理论上说，垂直的优势是当顾客认知打造出来以后，可以提升顾客忠诚度，从而降低营销成本。可现在没等到忠诚，钱就不够烧了。所以app的出现，从根源解决了这个问题。只要有好的产品，理论上，基本可以不用砸钱买流量。口碑传播，2的n次方的效果。

0的n次方等于0。

0的任何非0次方都是0，例：0=0×0×0×0×0=0；0的0次方无意义。

任何非零数的0次方都等于1。原因如下：

通常代表3次方，5的3次方是125，即5×5×5=125

5的2次方是25，即5×5=25

5的1次方是5，即5×1=5

由此n≧0时，将5的（n+1）次方变为5的n次方需除以一个5，所以5的0次方为：5 ÷ 5 = 1。

次方最基本的定义：

设a为某数，n为正整数，a的n次方表示为aⁿ，表示n个a连乘所得之结果，如2⁴=2×2×2×2=16。次方的定义还可以扩展到0次方、负数次方、小数次方、无理数次方甚至是虚数次方。

当m为正整数时，n^m指该式意义为m个n相乘。当m为小数时，m可以写成a/b(其中a、b为整数），n^m表示n^a再开b次根号。当m为虚数时，则需要利用欧拉公式 eiθ =cosθ+isinθ，再利用对数性质求解。

　　姓名：贺刚　体重：74KG　星座：巨蟹座　　爱好：计算机、唱歌、篮球　爱好：唱歌、运动、电脑　家庭成员：爸爸 妈妈 妹妹

　　最爱的人：爸爸 妈妈　最喜欢的事：和父母在一起分享成功的快乐　最喜欢的演员：刘德华、孙红雷　最喜欢的歌手：刘德华、张学友　最喜欢的漫画：七龙珠 阿拉蕾　最喜欢的城市：平遥 广州 深圳 北京　最喜欢的食物：排骨、土豆　最喜欢的水果：西瓜　最喜欢的饮料：西瓜汁、牛奶　最大的理想：事业成功后带着父母环游全世界

　　主要从艺经历

　　2002年8月，参加福建东南台开心一百明星脸周冠军、季冠军、年度亚军、最受欢迎明星脸；　2002年12月，清华同方全国数码活动冠军；　长治、晋城、济南、太原等多家电视台春节晚会嘉宾节目录制；　《十面埋伏》厦门首映式表演嘉宾 东南台全省巡演；　广州大方咏嘉化妆品公司“LACASTA品牌”全国推广演出；　2005年度参加“梅艳芳菲”大型模仿秀，模仿刘德华，成为全国总冠军，获最佳模仿奖和最佳人气奖；　2005年底参加拍摄电视连续剧《天地传奇》

　　2006年拍摄电视连续剧《梅艳芳菲》；　2007年参演电视剧《金婚》。　2008年参演《妈妈为我嫁》　2009年参演电视剧《流星蝴蝶剑》　2010年参演电视剧《家，n次方》　2010年参演央视开年大剧《第五空间》　2010年参演电视剧《极品妈妈》　2011年参演电视剧《卜案》　2011年参演电视剧《家，N次方》

矩阵n次方的公式是n=α^Tβ。

先求特征值和特征向量，得到一个特征值组成的对角矩阵Λ和一个可逆矩阵P，再求这个可逆矩阵的逆矩阵P^（-1），于是A^10=P^（-1）×（Λ^10）×P。当a^（n-1）b乘以a即变为a^nb，当a^n乘以-b即变为a^nb，前后两项异号相互抵消，最后乘下a^n-b^n。

矩阵n次方的算法：

先算两次方，三次方，最多算到4次方，就可以知道n次方，严格证明需要用数学归纳法。两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵。对称矩阵的正定性与其特征值密切相关。矩阵是正定的当且仅当其特征值都是正数。

a^n-b^n =(a-b)[a^(n-1)+a^(n-2)b+a^(n-3)b^2+……+ab^(n-2)+b^(n-1)]。

这个定理在遗传学中也有其用武之地，具体应用范围为：推测自交后代群体的基因型和概率、推测自交后代群体的表现型和概率、推测平衡状态群体的基因或基因型频率等。

次方最基本的定义是：设a为某数，n为正整数，a的n次方表示为aⁿ，表示n个a连乘所得之结果，如2⁴＝2×2×2×2=16。次方的定义还可以扩展到0次方、负数次方、小数次方、无理数次方甚至是虚数次方。

在电脑上输入数学公式时，因为不便于输入乘方，符号“＾”也经常被用来表示次方。例如2的5次方通常被表示为2^5。

二项式定理（英语：Binomial theorem），又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂，即广义二项式定理。

二项式定理最初用于开高次方。在中国，成书于1世纪的《九章算术》提出了世界上最早的多位正整数开平方、开立方的一般程序。11世纪中叶，贾宪在其《释锁算书》中给出了“开方作法本原图”（如图1），满足了三次以上开方的需要。此图即为直到六次幂的二项式系数表，但是，贾宪并未给出二项式系数的一般公式，因而未能建立一般正整数次幂的二项式定理。

x的n次方是幂函数。

函数x的n次方是幂函数，它的自变量的取值范围是全体实数，当n=0时y=x的0次方＝1，此时x不能等于0，它的图象是一条直线，过虚点（0，1)，平行于x轴；当n不等于0时，x取全体实数，当n<0时，它的图象是双曲线，关于原点对称；当n>0时，它的图象是一条曲线过点（0，0)。

什么是幂函数：

幂函数是基本初等函数之一。一般地。形如y=x（α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。例如函数y=x、y=x、y=x、y=x注：y=x=1/x y=x时x≠0等都是幂函数。

幂函数都过（1，1）。可以从函数从看出来函数的奇偶性，单调性。函数叫做幂函数，其中x是自变量，a是常数。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

幂通俗的说就是我们通常所说的多少次方，比如平方叫二次幂，立方叫三次幂，幂的大小是整数，不能是分数和小数

设a为某数，n为正整数，a的n次方表示为aⁿ，表示n个a连乘所得之结果，如2⁴=2×2×2×2=16。次方的定义还可以扩展到0次方和负数次方等等。

在电脑上输入数学公式时，因为不便于输入乘方，符号“^”也经常被用来表示次方。例如2的5次方通常被表示为2^5。

扩展资料：

次方有两种算法。

第一种是直接用乘法计算，例：3⁴=3×3×3×3=81

第二种则是用次方阶级下的数相乘，例：3⁴=9×9=81

(1) 任何不等于零的数的零次幂都等于1。

即  (a≠0)。

(2)任何不等于零的数的-p（p是正整数）次幂，等于这个数的p次幂的倒数。

即  (a≠0，p是正整数)。

（规定了零指数幂与负整数指数幂的意义，就把指数的概念从正整数推广到了整数。正整数指数幂的各种运算法则对整数指数幂都适用。）