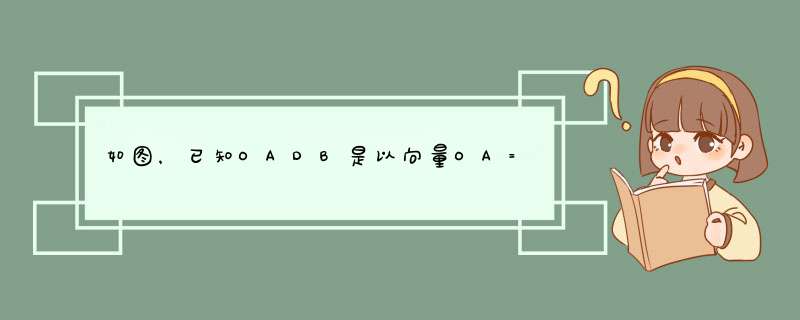
已知OADB是以向量OA=a,OB=b为邻边的平行四边形,OD与AB相交与C,且BM=(1/3)BC,
CN=(1/3)CD,用a,b表示一下向量:
1OM;2ON;3MN
解:1。OM=OB+BM=OB+(1/3)BC=OB+(1/6)BA=OB+(1/6)(OA-OB)
=(1/6)OA+(5/6)OB=(1/6)(OA+5OB)=(1/6)(a+5b)
2 ON=OC+CN=(1/2)OD+(1/3)CD=(1/2)(OA+OB)+(1/6)OD=(1/2)(OA+OB)+(1/6)(OA+OB)
=(2/3)(a+b)
3MN=MC+CN=(2/3)BC+(1/3)CD=(1/3)BA+(1/6)OD=(1/3)(OA-OB)+(1/6)(OA+OB)
=(1/2)OA-(1/6)OB=(1/2)a-(1/6)b
解:因为ABDE为圆内接四边形,因此对角互补(如果需要证明请提示)
则∠A+∠BDE=180。
因为∠CDE+∠BDE=180
所以,∠A=∠CDE
又,∠C=∠C。
所以△ABC∽△DEC
AB=AC=5,所以DE=CD=√5
且两三角形相似比为:DE:AB=1:√5
连接AD。
因为AB为直径,所以∠ADB=90(直径所对圆周角)。因此,AD⊥BC。
又因为△ABC为等腰三角形,因此AD也是底边BC中线。
则,BC=2CD=2√5
CE:BC=DE:AB=1:√5
所以CE=2
AE=AC-CE=5-2=3
DF=2
| 2 |
如图所示,延长DC、AE相交于点G,连接BG,过点B作BH⊥DG于点H,过点F作FM⊥DG于点M,
∴四边形ABHN是平行四边形,
∴BH=AN,
∵∠BDC=∠ADC-∠ADB=30°,
∴BD=2BH=2BN,
∵∠DAG=90°,∠ADG=45°,
∴DG=
| 2 |
| 2 |
| 2 |
∴DB=DG,
∴∠DBG=∠DGB=75°,
∴∠EBG=∠FBG-∠DBC=60°,∠BGF=30°,
∴BG=2BE=2AE,∠BFG=75°=∠FBG,
∴FG=BG=2AE,
∵DF=2FM,FG=
| 2 |
∴DF=
| 2 |
| 2 |
当adb push apk /system/app的时候出现Read-only file system的时候adb shell mount -o remount / /
android adb shell命令使用
当运行一个命令的时候出现
rm failed for CoeeRoatapk, Read-only file system
adb shell mount -o remount rw /system 挂载设备
内置应用:
adb shell mount -o remount rw /system
adb push clockapk /system/app/clockapk
删除内置应用:
adb shell mount -o remount rw /system
adb shell
cd system/app
rm -rf clockapk
bat 文件:
adb shell mount -o remount,rw /dev/block/mtdblock3 /system
adb push sssss /system/bin/rota
adb shell sync
adb shell chown rootshell /system/bin/rota
adb shell chmod 6755 /system/bin/rota
adb shell rm -r /system/xbin/sssss
adb shell sync
adb shell ln -s /system/bin/sssss /system/xbin/sssss
adb shell sync
adb shell mount -o remount,ro /dev/block/mtdblock3 /system
pause
答:△EFG是等边三角形。
理由如下:
如图,连接DE、CF则:
EF=(1/2)AB=(1/2)DC,
由∠ADB=60°得知:三角形AOD和三角形BCO都是等边三角形。又E、F分别是AO,BO 的中点,
所以:DE和CF分别垂直AC和BD
而G点是直角三角形EDC和直角三角形DFC的公共斜边的中点。
所以:EG=FG=(1/2)DC=EF
因此:△EFG是等边三角形
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
