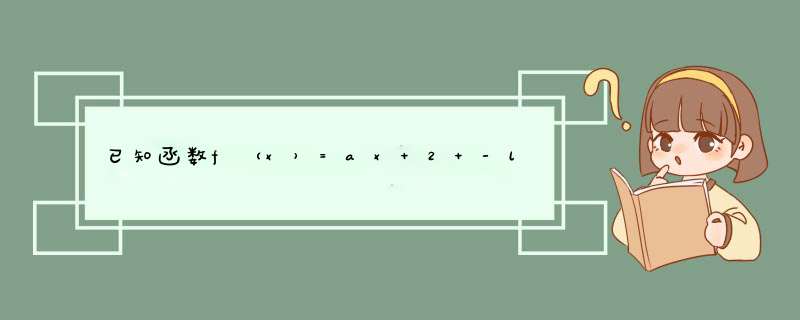
| (Ⅰ)f(x)的定义域为(0,+∞), 由f(x)=ax 2 -lnx,得:f′(x)=2ax-
(1)若a≤0,则f′(x)<0,f(x)在(0,+∞)是减函数; (2)若a>0,由 f ′ (x)=2ax-
则当x∈(0,
当x∈(
(Ⅱ)证明:曲线y=f(x)在P(t,f(t))处的切线方程为y=f′(t)(x-t)+f(t), 且P为它们的一个公共点. 当a= -
设g(x)=f(x)-[f′(t)(x-t)+f(t)],则g′(x)=f′(x)-f′(t), 则有g(t)=0,且g′(t)=0. 设h(x)=g′(x)=-
于是g′(x)在(0,2)是增函数,且g′(t)=0, 所以,当x∈(0,t)时,g′(x)<0,g(x)在(0,t)是减函数; 当x∈(t,2)时,g′(x)>0,g(x)在(t,2)是增函数. 故当x∈(0,t)或x∈(t,2]时,g(x)>g(t)=0. 若x∈(2,+∞),则g(x)=-
=-
当x>2t+
所以在区间(2,2t+
因此曲线y=f(x)与其在点P(t,f(t))处的切线至少有两个不同的公共点. |
(Ⅰ)当a=-1时,f(x)=-x+lnx,f′(x)=1+
| 1 |
| x |
| x +1 |
| x |
对于x∈(0,1),有f'(x)>0,∴f(x)在区间(0,1]上为增函数,
对于x∈(1,+∞),有f'(x)<0,∴f(x)在区间(1,+∞)上为减函数,.
∴fmax(x)=f(1)=-1;
(II)直线P1P2的斜率为 k=
| ax2+lnx2ax1lnx1 |
| x2x1 |
| lnx2lnx1 |
| x2x1 |
由(1)知-x+lnx≤-1,当且仅当x=1时取等号,
∴
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2x1 |
| x1 |
| lnx2lnx1 |
| x2x1 |
| 1 |
| x1 |
同理,由
| x1 |
| x2 |
| x1 |
| x2 |
| lnx2lnx1 |
| x2x1 |
| 1 |
| x2 |
故P1P2的斜率 k∈(a+
| 1 |
| x2 |
| 1 |
| x1 |
又在x∈(x1,x2)上,f′(x)=a+
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x1 |
所以f(x)图象上存在点P0(x0,y0),满足x1<x0<x2,且f(x)图象上以P0为切点的切线与直线P1P2平行;
(III)f(x)=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 1 |
| an |
a3=
| 3 |
| 2 |
| 1 |
| a2 |
| 3 |
| 2 |
| 1 |
| a3 |
| 3 |
| 2 |
| 1 | ||||
|
| 13a2+6 |
| 2(3a2+2) |
(2a2+1)(a2-1)>0a2>2
| 3 |
| 2 |
| 1 |
| a1 |
下面我们证明:当0<a1<2时,a2n+2<a2n,且a2n>2(n∈N+)
事实上,当n=1时,0<a1<2a2=
| 3 |
| 2 |
| 1 |
| a1 |
a4-a2=
| 13a2+6 |
| 2(3a2+2) |
| 3(2a2+1)(a22) |
| 2(3a2+2) |
若当n=k时结论成立,即a2k+2<a2k,且a2k>2,则
a2k+2=
| 3 |
| 2 |
| 1 |
| a2k |
| 3 |
| 2 |
| 1 |
| a2k+2 |
a2k+4-a2k+2=
| 13a2k+2+6 |
| 2(3a2k+2+2) |
| 3(2a2k+2+1)(a2k+22) |
| 2(3a2k+2+2) |
a2k+4<a2k+2,
由上述证明可知,a1的取值范围是(0,2).
∫(上限为正无穷,下限为2)1/x(lnx)^kdx
=∫1/(lnx)^k d lnx (x上限为正无穷,下限为2)
=1/(1-k)∫d(lnx)^(1-k) (x上限为正无穷,下限为2)
=[1/(1-k)][(ln正无穷大)^(1-k)-1]
若广义积分收敛,所以1-k小于0
所以k大于1
若广义积分发散,k小于等于1
当k=1时取最小值
解:(1)g(x)=2/x+lnx
定义域x>0
g'(x)=-2/x²+1/x=(x-2)/x²
驻点:x=2
0<x<2,g'(x)<0,g(x)单调递减
x>2,g'(x)>0,g(x)单调递增
∴x=2,是极小值点。
(2)令i(x)=f(x)-g(x)=mx-(m-2)/x-lnx-2/x-lnx=mx-m/x-2lnx
i'(x)=m+m/x²-2/x=(mx²-2x+m)/x²
令j(x)=mx²-2x+m x≥1
m=0,j(x)=-2x,x≥1,j(x)≤-2,i'(x)<0,i(x)单调递减,成立
j(x)=mx²-2x+m 零点
x=(1±√1-m²)/m
当右零点≤1或零点不存在(|m|>1)时,x∈[1,+∞),j(x)恒大于或小于0,i(x)为单调函数
0<m≤1时,右零点(1+√1-m²)/m≤1 m=1
m<0时,右零点(1-√1-m²)/m≤0<1 恒成立
∴m的取值范围是m≥1∪m≤0
(3)令k(x)=f(x)-g(x)-h(x)=mx-(m+2e)/x-2lnx
k'(x)=m+(m+2e)/x²-2/x=[mx²-2x+(m+2e)]/x²
当Δ=4-4m²-8em<0→m>√(4e²+1)-4e或m<-√(4e²+1)-4e时,k(x)为单调函数
k(1)=m-1-2e
k(e)=me-5
当m<-√(4e²+1)-4e时,k(1)、k(e)<0→k(x)<0,无解
m>√(4e²+1)-4e
k(1)=m-1-2e>0 →m>1+2e
k(e)=me-5>0 →m>5/e
即m>5/e,至少有x₀=e,使得k(x₀)>0
当Δ≥0时,即-√(4e²+1)-4e<m√(4e²+1)-4e<0
存在驻点:x=(1±√1-m²-2em)/m <0,不在区间内
∴m的取值范围为:m>5/e
解由f(x)=x+alnx知x>0求导的f'(x)=1+a/x(x>0)知当a≥0时,f'(x)>0即f(x)是增函数,此时增区间为(0,正无穷大)当a<0时,令f'(x)=1+a/x=0即(x+a)/x=0解得x=-a由当x属于(0,-a)时,f'(x)=1+a/x=(x+a)/x<0当x
解由f(x)=x+alnx知x>0
求导的f'(x)=1+a/x(x>0)
知当a≥0时,f'(x)>0
即f(x)是增函数,此时增区间为(0,正无穷大)
当a<0时,
令f'(x)=1+a/x=0
即(x+a)/x=0
解得x=-a
由当x属于(0,-a)时,f'(x)=1+a/x=(x+a)/x<0
当x属于(-a,正无穷大)时,令f'(x)=1+a/x=(x+a)/x>0
即f(x)的单调减区间为(0,-a),增区间为(-a,正无穷大)。
故综上知a≥0时,增区间为(0,正无穷大)
当a<0时,f(x)的单调减区间为(0,-a),增区间为(-a,正无穷大)。
(1)由效用函数知U=1/3lnx+2/3lny得,MUx=1/3x MUy=2/3y
根据消费者均衡条件MUx/px=MUy/Py
XPx+YPy=I,所以X=I/3Px,Y=2I/Py
(2)根据上面需求函数,当I=600,
P_=Py=2得x=100,y=200
:
影响价格因素有很多,那么商品价格受什么因素影响呢
商品价格受影响:
影响价格的因素有很多种,其中间接因素有时间,地域,气候,政策,生产条件,习俗,消费心理等。这些都是通过改变商品的价格来影响供求关系的。而影响商品价格的最重要因素是:
1、价值决定价格;
2、供求关系影响价格;
3、其他因素。
价值决定价格:
在价格受什么因素影响中,价值规律是商品的价值量由生产该商品的社会必要劳动时间决定,商品交换必须以价值量为基础,实行等价交换。价值规律作用主要表现在以下几个方面:
(1)价值规律调节社会经济资源即社会劳动在各生产部门之间的分配;
(2)价值规律对商品流通的调节主要是通过价格围绕价值上下波动引起商品供求关系变化来实现的;
(3)价值规律促使企业改进生产技术,改善经营管理,提高劳动生产率和经济效益。价值与价格的关系:价价值决定价格,价格是价值的货币表现。所以要是说价格受什么因素影响的话,货币表现占很大的因素。
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
