在三角形ABC中,角C=90,AB=10,AC=6,点O是AB的中点,将一块直角三角板绕点O旋转，N、M分别时直角三角形

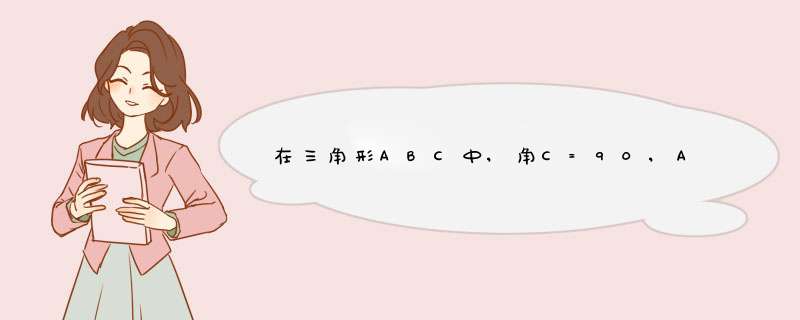
在⊿ABC中,∠C=90º,，AB=10，AC=6，点O是AB的中点；

将一块直角三角板的直角顶点绕点O旋转，M、N分别为

直角三角板的直角边与AC，BC的交点。

（1）如图①，

①当M与A重合时，求CN的长。②写出AC²，CN²,，BN²的数量关系 。

（2）当三角板顺时针旋转，使点M在AC上（不与A、C重合），

写出AM²,CM²，CN²，BN²的数量关系 。

提示：

⑴ ﹙CN＝7／4，AM²＋CN²＝BN²﹚

⑵延长MO至M′，使OM′＝MO，连接MB′，

易证⊿AOM≌⊿BOM′﹙SAS﹚，

∴AM＝BM′，∠A＝∠BM′O，

∴M′B∥AC，

又AC⊥BC，

M′B⊥BC；

连NM，NM′，

 MO＝OM′，NO⊥MM′，

∴NM＝NM′，

NM²＝CM²;＋CN²，

NM′²＝M′B²＋BN²，

∴CM²＋CN²＝M′B²＋BN²，

又M′B＝AM，

∴CM²＋CN²＝AM²＋BN²，

如图,AB//CD,点E是AB上方一点,MF平分∠AME,若点G恰好MF的反向延长线上,且NE平分∠CNG，2∠E与∠G互余， 

求∠AME的大小。

问题补充： 

(2)如图，在（1）的条件下，若点P是EM上一动点。PQ平分∠MPN，NH平分∠PNC，交AB于点H,PJ//NH,当点P在线段EM上运动时，∠JPQ的度数是否改变？若不变，求出其值；若改变，请说明你的理由。

如图连接AO，OB，OP则OM，OP，ON分别平分∠AOP，∠APB，∠BOC

则∠APO=1/2∠APB=28°

又∵AP为圆o的切线

∴OA⊥AP，即∠OAP=90

∴∠AOP=180°-∠APO-∠OAP

             =180°-28°-90°

             =62°

又∵OM平分∠AOP

∴∠MOP=1/2∠AOP

               =31°

同理可得∠PON=31°

所以∠MON=62°

连接MN,过M点作直线MO平行于DC,且交PD于O点,连接OA

则MO为三角形PDC的中位线

所以MO平行且等于1/2DC

因为N为AB中点

所以平行且等于1/2DC

所以四边形AOMN为平行四边形

所以MN平行于OA,AN平行于MO

因为PA垂直平面ABCD

所以PA垂直于AB,且PA垂直于AD

因为ABCD为矩形

所以AB垂直于AD

因为PA属于平面PAD,AD也属于平面PAD,PA、AD交于A点

所以BA垂直于平面PAD

所以BA垂直于OA

因为AN平行于MO

所以OA垂直于MO

因为PA=AD

所以三角形PAD为等腰三角形

因为O为PD中点

所以OA垂直于PD

因为OM交PD于O

所以OA垂直于平面PAC

因为MN平行于OA

MN垂直平面CD

解法一：如图1所示，过O作OF⊥BC，过A作AM⊥OF，

∵四边形ABDE为正方形，

∴∠AOB=90°，OA=OB，

∴∠AOM+∠BOF=90°，

又∠AMO=90°，∴∠AOM+∠OAM=90°，

∴∠BOF=∠OAM，

在△AOM和△BOF中，

∠AMO=∠OFB=90°∠OAM=∠BOFOA=OB，

∴△AOM≌△BOF（AAS），

∴AM=OF，OM=FB，

又∠ACB=∠AMF=∠CFM=90°，

∴四边形ACFM为矩形，

∴AM=CF，AC=MF=5，

∴OF=CF，

∴△OCF为等腰直角三角形，

∵OC=62，

∴根据勾股定理得：CF2+OF2=OC2，

解得：CF=OF=6，

∴FB=OM=OF-FM=6-5=1，

则BC=CF+BF=6+1=7．

故答案为：7．

解法二：如图2所示，

过点O作OM⊥CA，交CA的延长线于点M；过点O作ON⊥BC于点N．

易证△OMA≌△ONB，∴OM=ON，MA=NB．

∴O点在∠ACB的平分线上，∴△OCM为等腰直角三角形．

∵OC=62，∴CM=6．

∴MA=CM-AC=6-5=1，

∴BC=CN+NB=6+1=7．

连接OP

因为P，M关于OA对称，则OA是PM的垂直平分线，

所以，OM=OP

同理，P,N关于OB对称，则OB是PN的垂直平分线，

所以，ON=OP

在三角形OPM中，OA垂直于PM，而OP=OM

所以，<MOA=<POA

同理，<NOB=<POB

由于<POA+<POB=<AOB=30º

所以，<MOA+<NOB=30º

因此，<MON=60º

于是，三角形MON是等边三角形

1）平面ABCD垂直于平面ABEF,ABCD是矩形，所以CB垂直于AB，CB垂直于平面ABEF，所以CB垂直于AF，同时AF垂直于BF，CB与BF相交，所以AF垂直于平面CBF

2）做DF的中点N，连接MN，可得MN//CD且MN=CD/2，因为AO//CD且AO=CD/2，所以AO//=MN，所以AOMN是平行四边形，那么OM//AN,AN是平面DAF上的一条线，所以OM//平面DAF

3）三角形BEF的面积会求不？

提示一下，AF垂直于BF，可以得到BF=根号3，EF=1，梯形的高(根号3)/2,三角形BEF的面积S=（根号3）/4，三棱锥C-BEF的高即为CB=1，所以体积V=SCB/3=(根号3）/12