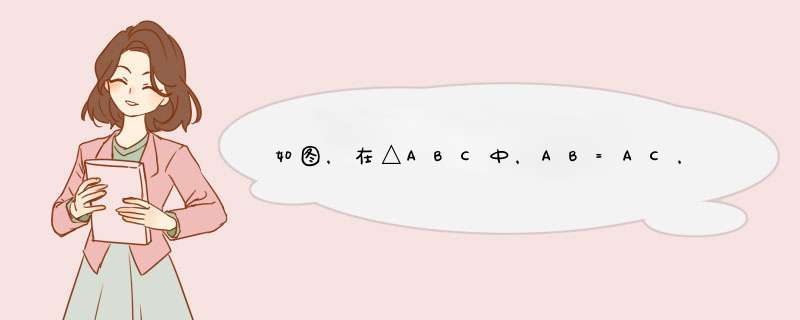
3 BC²=2AB×CE
证明:
(1)连接AD
∵AB是直径
∴∠ADB=90º,即AD⊥BC
∵AB=AC
∴AD平分BC三线合一,即D是BC的中点
(2)
连接BE
∵AB是直径
∴∠AEB=90º
则∠BEC=∠ADC=90º
又∵∠BCE=∠ACD公共角
∴⊿BEC∽⊿ADC(AA)
(3)
∵⊿BEC∽⊿ADC
∴BC/AC=CE/CD
转化为BC×CD=AC×CE
∵CD=½BC,AB=AC
∴BC²=2AB×CE
1、三角形ABD为直角三角形,三角形ABC等腰三角形,所以BD=DC所以OD平行AC,得第一证
2、角AGC为60度,可证的三角形AGC为等边三角形。
很简单的,就是画图大啊
(1)证明:连接OD.
∵AB=AC,∴∠C=∠B. (1分)
∵OD=OB,∴∠B=∠1.
∴∠C=∠1. (2分)
∴OD∥AC,∴∠2=∠FDO. (3分)
∵DF⊥AC,∴∠2=90°,∴∠FDO=90°,
即FD⊥OD.
∴FD是圆O的切线. (4分)
(2)解:∵AB是⊙O的直径,∴∠ADB=90°. (5分)
∵AC=AB,∴∠3=∠4. (6分)
∴ ED^= DB^,∵ AE^= DE^,∴ DE^= DB^= AE^. (7分)
∴∠B=2∠4,∴∠B=60°,∠5=120°,
∴△ABC是等边三角形,∠C=60°. (8分)
在Rt△CFD中,sinC= DFCD,CD= 2sin60°= 232= 433,
∴DB= 433,AB=BC= 833∴AO= 433. (9分)
∴ lAD^= nπR180= 839π. (10分)
解:(1)圆的切割线定理,求得圆的半径。
CD的平方=CACB
(3R)的平方=1(1+2R),解得R=(1+根号10)/9
(2)阴影面积由弓形面积与三角形的面积组合而成,在动点变化的过程中,弓形面积保持不变,而三角形的面积由于同底等高也保持不变,所以阴影面积保持不变。
既然保持不变,那么选取最简单的特殊情况求取面积值,即阴影为扇形时,即Q点到圆心O。在直角三角形OCD中,角AOD的正切值为CD/OD=3R/R=3,则角AOD=反正切值3所代表的角度=arctg3=角BOE,则角DOE=派-2arctg3
所以扇形DOE的面积S=弧DER=圆心角的弧度数半径的平方
=(派-2arctg3)(1+根号10)的平方/81
阴影部分的面积是32CM²
S阴影=1/2 S圆O-S弓形ADB
图解
数据
∵△ABC为直角三角形
∴AB为圆o的直径 即OA=8
∴等腰直角三角形OAC的斜边AC=8根号2(根据等腰直角三角形边的比列1:1:根号2)
解答步骤
1/2S圆O= 1/2πR²
=32π
2S弓形ADB=1/4 S圆C-S△ACB
圆C的半径r=AC=8根号2
1/4 S圆C=1/4 πr²=32π
S△ACB=1/2ACBC=32
S弓形ADB=1/4 S圆C-S△ACB
=32π-32
S阴影=1/2 S圆O-S弓形ADB
=32π-32π+32
=32CM²
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
