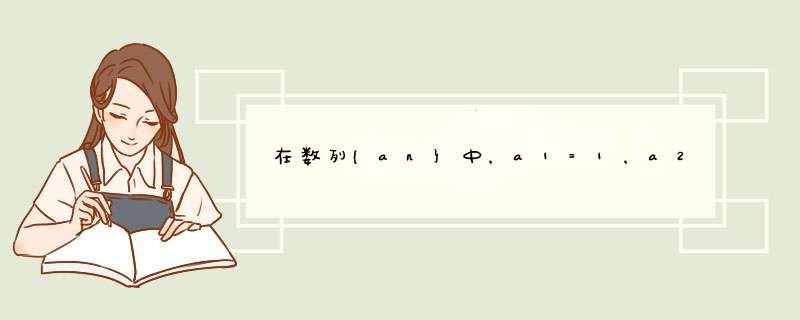
解答:解:(1)∵a1=1,a2=3,
a3=3×3-k×1=9-k,
a4=3×(9-k)-k×3=27-6k,
∵bn=an+1-an,
∴b1=3-1=2,b2=6-k,b3=18-5k,
∵{bn}成等比数列,
∴b22=b1•b3,
∴(6-k)2=2×(18-5k),
解得k=2或k=0(舍)
当k=2时,an+2=3an+1-2an,
∴an+2-an+1=2(an+1-an),
∴
bn+1
bn
=2,∴k=2时满足条件
(2)∵b1=2,{bn}成等比数列,
bn+1
bn
=2,∴bn=2n,
∴a2-a1=2,a3-a2=22,…,an-an-1=2n-1,
∴an-a1=1+2+22+23+…+2n-1
=
1-2n
1-2
=2n-1,
∴an=2n
(3)Sn=b1+2b2+3b3+…nbn
=1•2+2•22+3•23+…+n•2n,①
2Sn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-Sn=2+22+23+…+2n-n×2n+1
=
2(1-2n)
1-2
-n×2n+1
=2n+1-2-n×2n+1,
∴Sn=(n-1)×2n+1+2
解:(1)当k=1时,S
n
=a
n
+n
2
-n,
∴S
n-1
=n
2
-n,(n≥2),
∴S
n
=(n+1)
2
-(n+1)=n
2
+n(n≥1)
∴当n=1时,a
1
=S
1
=2;
当n≥2时,a
n
=S
n
-S
n-1
=n
2
+n-(n-1)
2
-(n-1)=2n,
所以数列{a
n
}的通项公式为a
n
=2n(n∈N
).
(
II)当n≥2时,a
n
=S
n
-S
n-1
=ka
n
-ka
n-1
+2n-2,
∴(k-1)a
n
=ka
n-1
-2n+2,a
1
=S
1
=ka
1
,
若k=1,则a
n
-2n-1=-1,
从而{a
n
-2n-1}为公比为1的等比数列,不合题意;
若k≠1,则a
1
=0,a
2
=
2
1-k
,a
3
=
4-6k
(1-k)2
,a
1
-3=-3,a
2
-5=
5k-3
1-k
,a
3
-7=
-7k2+8k-3
(k-1)2
,
由题意得,(a2-5)2=(a
1
-3)(a
3
-7)≠0,
∴k=0或k=
3
2
,
当k=0时,S
n
=n
2
-n,a
n
=2n-2,a
n
-2n-1=-3,不合题意;
当k=
3
2
时,a
n
=3a
n-1
-4n+4,从而a
n
-2n-1=3[a
n-1
-2(n-1)-1],
∵a
1
-2×1-1=-3≠0,a
n
-2n-1≠0,{a
n
-2n-1}为公比为3的等比数列,
∴a
n
-2n-1=-3
n
,
∴a
n
=2n-3
n
+1,
∴S
n
=n
2
+2n-
3n+1
2
+
3
2
.
由 a_(n+1) = ka_(n) + b
a_(n+1) + p = k( a_(n) + p )
则 p = b/(k-1)
{a_(n) + p} 为首先是a+p,公比为k的等比数列
故 a_(n) + p = (a+p)k^(n-1)
a_(n) = (a+p)k^(n-1) - p = (a+b/(k-1))k^(n-1) - b/(k-1)
Sn=kan+1
n>=2
时
S(n-1)=ka(n-1)+1
Sn-S(n-1)=an=kan+1-ka(n-1)-1=k(an-a(n-1))
(k-1)an=ka(n-1)
an/a(n-1)=k/(k-1)
所以为等比数列
其实不够准确
s1=a1=ka1+1
S2=a1+a2=ka2+1
验证
a2/a1是否等于k/(k-1)即可
望采纳
由an+1=kan+3(k>0),且a1=0,a4=9,
得a2=ka1+3=3,
a3=ka2+3=3k+3,
a4=9=ka3+3=k(3k+3)+3,
解得:k=-2或k=1,
∵k>0,
∴k=1.
故选:A.
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
