∫cosnxdx递推公式

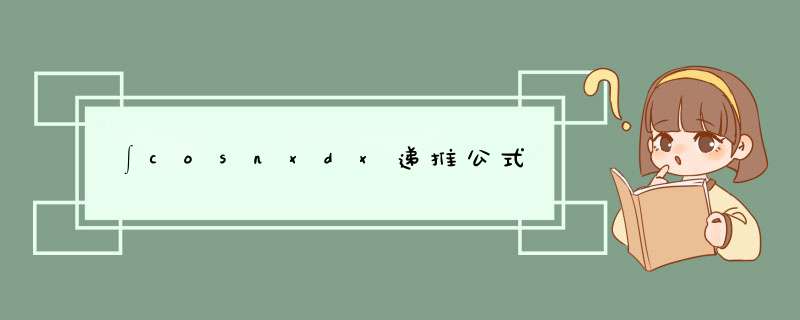
IN(下标）=∫x^n cosxdx

=∫x^n dsinx =x^n sinx-∫ sinx dx^n

=x^n sinx-n∫ sinx(x(n-1)dx

=x^n sinx+n∫x^(n-1) dcosx

=x^n sinx+nx^(n-1) cosx-n(n-1)∫x(n-2) cosx dx

IN(下标）=x^n sinx+nx^(n-1) cosx-n(n-1)In-2(下标）

I₅=x⁵ sinx+5x⁴ cosx-20 I₃

且I₃=x³ sinx+3x² cosx-6I₁

I₁=∫x cos x dx = ∫x dsinx

=xsinx-∫ sinx dx

=x sinx + cosx +c

再将I₁、I₃回代可得I₅

扩展资料：

微积分的基本公式共有四大公式

1、牛顿-莱布尼茨公式,又称为微积分基本公式；

2、格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分；

1、inx的不定积分是∫lnxdx=xlnx-∫xdlnx=xlnx-∫dx=xlnx-x+C。在微积分中，一个函数f的不定积分，或原函数，或反导数，是一个导数等于f的函数F，即F′=f。

2、不定积分和定积分间的关系由微积分基本定理确定。其中F是f的不定积分。根据牛顿-莱布尼茨公式，许多函数的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关系：定积分是一个数，而不定积分是一个表达式，它们仅仅是数学上有一个计算关系。一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。连续函数，一定存在定积分和不定积分；若在有限区间[a,b]上只有有限个间断点且函数有界，则定积分存在；若有跳跃、可去、无穷间断点，则原函数一定不存在，即不定积分一定不存在。

∫ln(1+x)dx

=x·ln(1+x)-∫xd[ln(1+x)]——分部积分法

=x·ln(1+x)-∫[x/(1+x)]dx

=x·ln(1+x)-∫[(x+1)-1]/(1+x)dx

=x·ln(1+x)-∫[1-(1/1+x)]dx

=x·ln(1+x)-x+ln(1+x)+C

扩展资料

证明：如果f(x)在区间I上有原函数，即有一个函数F(x)使对任意x∈I，都有F'(x)=f(x)，那么对任何常数显然也有[F(x)+C]'=f(x)。即对任何常数C，函数F(x)+C也是f(x)的原函数。这说明如果f(x)有一个原函数，那么f(x)就有无限多个原函数。

设G(x)是f(x)的另一个原函数,即∀x∈I，G'(x)=f(x)。于是[G(x)-F(x)]'=G'(x)-F'(x)=f(x)-f(x)=0。

由于在一个区间上导数恒为零的函数必为常数，所以G(x)-F(x)=C’(C‘为某个常数)。

这表明G(x)与F(x)只差一个常数，因此，当C为任意常数时，表达式F(x)+C就可以表示f(x)的任意一个原函数。也就是说f(x)的全体原函数所组成的集合就是函数族{F(x)+C|-∞<C<+∞}。

由此可知，如果F(x)是f(x)在区间I上的一个原函数，那么F(x)+C就是f(x)的不定积分，即∫f(x)dx=F(x)+C。

因而不定积分∫f(x) dx可以表示f(x)的任意一个原函数。

win10安装系统盘问题造成，比如系统盘是损坏的。

解决方法：更换win10安装系统盘，重新安装win10系统。

win10安装过程中，操作不对造成的。解决方法：必须正确安装win10系统。

IN AL,DX(DX是源操作数。AL是8位寄存器，作为目的操作数，IN指令是端口操作指令，作用是将源操作数代表的端口的内容送给目的操作数，所以整条指令是将DX端口的内容送给AL寄存器）

实际上indx是数据表的偏移地址，在查表指令FND中你会看得见。

对于TABLE FIND指令

表格查找（TBL）指令在表格（TBL）中搜索与某些标准相符的数据。"表格查找"指令搜索表，从INDX指定的表格条目开始，寻找与CMD定义的搜索标准相匹配的数据数值（PTN）。命令参数（CMD）被指定一个1至4的数值，分别代表 =、<>、<, and >。如果找到匹配条目，则INDX指向表格中的匹配条目。欲查找下一个匹配条目，再次激活"表格查找"指令之前必须在INDX上加1。如果未找到匹配条目，INDX的数值等于条目计数。