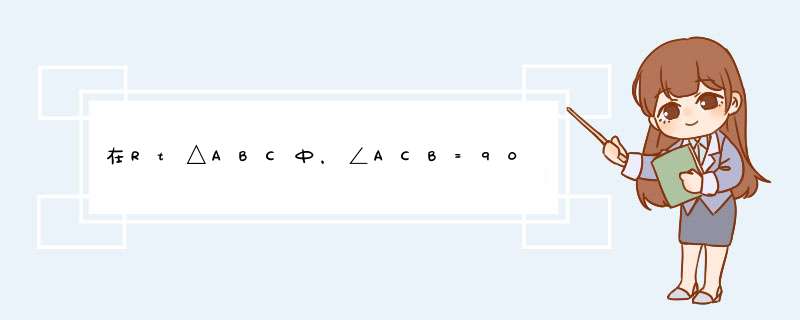
解答：（1）证明：如图1，∵CH⊥AB，
∴∠BHC=90°．．
又∠ACB=90°，
∴∠B=∠ACH，
∴∠DCE=∠B，
∴∠DCE=∠ACH，
∴∠DCH=∠KCE．
又sinB=
| CH |
| BC |
| 4 |
| 5 |
∴BC=
| 4 |
| 5 |
∵
| 4 |
| 5 |
∴CHCK=CDCE，即
| CE |
| CH |
| CK |
| CD |
∴△CEK∽△CHD，
∴∠DEC=∠DHC=90°，
∴∠CED=90°；
（2）BG-BC=
| 15 |
| 16 |
①如图2，当点D在线段BH上时．
故点D作DC的垂线交CE的延长线于点M，连接AM．
由（1）可知，∠DCM=∠ACH．
∴cos∠DCN=cos∠ACH，
∴
| CD |
| CM |
| CH |
| AC |
又∵∠DCH=∠MCA，
∴△CDH∽△CMA，
∴
| DH |
| AM |
| CH |
| AC |
| 3 |
| 5 |
∴∠MAC+∠BCA=180°，
∴MA∥BC，
∴∠AME=∠GCE，
又∠AEM=∠CEG．
∴△AME∽△GCE，
∴
| AM |
| GC |
| ME |
| EC |
又tan∠DCE=tan∠MDE=
| 4 |
| 3 |
∴
| DE |
| CE |
| ME |
| DE |
| 4 |
| 3 |
∴
| ME |
| EC |
| 16 |
| 9 |
∴
| AM |
| GC |
| 16 |
| 9 |
∴GC=
| 15 |
| 16 |
∴BG-BC=
| 15 |
| 16 |
②如图3，当点D在线段AH上时，同理可得 BG-BC=
| 15 |
| 16 |
欢迎分享，转载请注明来源：品搜搜测评网
微信扫一扫
支付宝扫一扫
