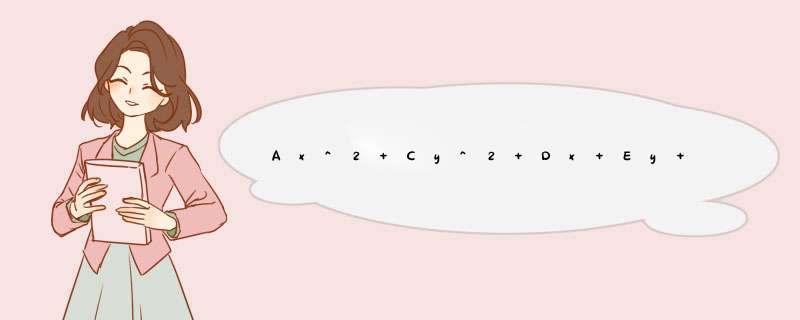
1A=C=0, 且D≠0,或E≠0时,表示直线;
2A=0,C≠0或C =0,A≠0时,且D≠0,或E≠0时,表示抛物线;
A=0,C≠0且D=E=0,CF<0时表示两条平行线;
或C =0,A≠0时,且D=E=0,AF<0时表示两条平行线;
3 A=C≠0且D^2+E^2-4AF>0时表示圆;A=C≠0且D^2+E^2-4AF=0时表示点;
A=C≠0且D^2+E^2-4AF<0时,不表示任何点。
4AC<0时,CD^2+AE^2-4ACF=0表示两条直线;
AC<0时,CD^2+AE^2-4ACF≠0表示双曲线直线;
5A≠C,AC>0时,(CD^2+AE^2-4ACF)A>0表示椭圆;
CD^2+AE^2-4ACF=0表示一点;(CD^2+AE^2-4ACF)A<0不表示任何点
x+y-ey=0
把y看成是关于x的函数y(x)
这样,对x求导
x+y'(x)-eyy'(x)=0
结果是
1+y'-eyy'=0
x/y=sin(xy)
必须始终把y看成关于x的函数,也就是y=y(x)
因为隐函数的解析式我们是无法求出来的,因此只能用y=y(x)代替
那么两边对x求导
根据复合函数求导公式
左边=[x'y(x)-xy'(x)]/[y(x)]^2
右边=cos(xy)[x'y(x)+xy'(x)]
所以左边=右边
得到[y-xy']/y^2=cos(xy)(y+xy')
y-xy'=y^2cos(xy)(y+xy')
xy'+xy^2y'cos(xy)=y-y^3cos(xy)
所以y'=[y-y^3cos(xy)]/[x+xy^2cos(xy)]
椭圆过右焦点的半径r=a-ex 过左焦点的半径r=a+ex 过上焦点的半径r=a-ey 过下焦点的半径r=a+ey 双曲线过右焦点的半径r=|ex-a| 双曲线过左焦点的半径r=|ex+a| 双曲线过下焦点的半径r=|ey+a| 双曲线过上焦点的半径r=|ey-a| 抛物线焦点x,开口右的半径r=p/2+x0;焦点x,开口左的半径r=p/2-x0;焦点y,开口上的半径r=p/2+y0;焦点y,开口下的半径r=p/2-y0 记忆方法: 椭圆的焦半径是左加,右减;下加,上减。双曲线的焦半径是左加套绝对值,右减套绝对值;下加套绝对值,上减套绝对值。
一般情况下的焦半径公式,及推导
1椭圆的焦半径公式
设M(xo,y0)是椭圆x2/a2+ y2/b2=1(a>b>0)的一点,r1和r2分别是点M与点F1(-c,0),F2(c,0)的距离,那么(左焦半径)r1=a+ex0,(右焦半径)r2=a -ex0,其中e是离心率。 推导:r1/∣MN1∣= r2/∣MN2∣=e 可得:r1= e∣MN1∣= e(a^2/ c+x0)= a+ex0,r2= e∣MN2∣= e(a^2/ c-x0)= a-ex0。 同理:∣MF1∣= a+ey0,∣MF2∣= a-ey0。
2双曲线的焦半径公式
双曲线的焦半径及其应用: 1:定义:双曲线上任意一点M与双曲线焦点的连线段,叫做双曲线的焦半径。 2.当点P在双曲线右支时的焦半径公式,(其中F1为左焦点,F2为右焦点)它是由第二定义导出的,其中a是实半轴长,e是离心率,x。是P点的横坐标|PF2|=ex。-a 并且只记右支,左支和右支只差一个负号 若焦点在y轴同理只记上支 双曲线过右焦点的半径r=|a-ex| 双曲线过左焦点的半径r=|a+ex|
3抛物线的焦半径公式
抛物线r=x+p/2</CA> 通径:圆锥曲线(除圆)中,过焦点并垂直于轴的弦 双曲线和椭圆的通径是2b^2/a焦准距为a^2/c-c 抛物线的通径是2p 抛物线y^2=2px (p>0),C(Xo,Yo)为抛物线上的一点,焦半径|CF|=Xo+p/2
同学你好,如果问题已解决,记得右上角采纳哦~~~您的采纳是对我的肯定~谢谢哦
是的,25年考研,但考试时间是24年 12月。
为大家整理了一份考研学习资料,包括公共课,数学,英语以及各大专业课的学习资源,后面会不断汇聚更多优秀学习资源,供大家交流分享学习,需要的可以先收藏转存,有时间慢慢看~
考研资料包实时更新
链接:https://panbaiducom/s/1fF6ey0j777BGYXENq1IoyA
pwd=1234提取码:1234
都很难的,需要提交准备
为大家整理了一份考研学习资料,包括公共课,数学,英语以及各大专业课的学习资源,后面会不断汇聚更多优秀学习资源,供大家交流分享学习,需要的可以先收藏转存,有时间慢慢看~
考研资料包实时更新
链接:https://panbaiducom/s/1fF6ey0j777BGYXENq1IoyA
pwd=1234提取码:1234
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
