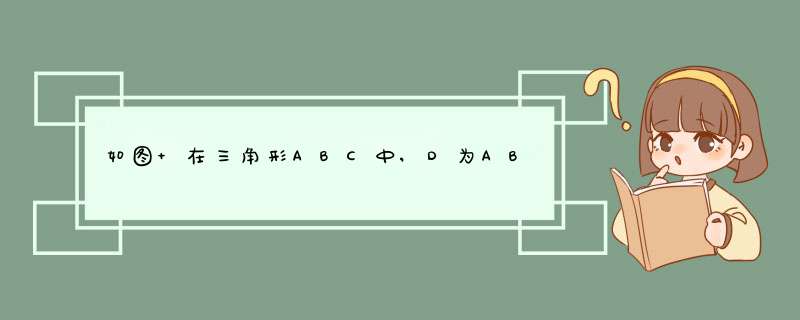
解答：如图，过C作CG平行AB，则
三角形EGC与EAD相似，有CG：AD=EC：AE，
三角形FCG与FBD相似，有CG：BD=CF：BF，
因AD=BD，所以，EC：AE=CF：BF，即：AECF=BFEC。
解：
在平行四边形ABCD中
AD=BC且AD//BC
E,F分别为AD,BC中点
AE=AD/2
BF=BC/2
AE=BF且AE//BF
AE:BF=EG:BG
有BG=EG
同理得EH=CH
即G,H分别为BE,CE的中点
GH为三角形BCE的中位线
所以GH=AD/2
证明：
（1）
AE‖BF
AE=BF
四边形ABFE为平行四边形
所以G为AF和BE的中点
同理
点H也是平行四边形FCDE中EC和FD的中点
在△AFD中
点G，H为两边中点
所以GH‖1/2AD
AD‖BC
AD=BC
GH‖BC
（2）
AD=BC
GH=1/2BC
欢迎分享，转载请注明来源：品搜搜测评网
微信扫一扫
支付宝扫一扫
妮维雅这个品牌大家都比较熟悉，很多人都会想到它们家的洗面奶，还经常被拿来和其他的护肤品牌做比较，比如说欧莱雅这个品牌，因为欧莱雅的护肤产和妮维雅一样也是有男士和女士的，那妮维雅和欧莱雅哪个好？妮维雅是哪国的品牌？1、妮维雅和欧莱雅哪个好妮维
天气丹护肤产品中包括很多款，针对皮肤的效果也是不一样的，在使用的时候一定要注意它的顺序，如果使用顺序错误很容易导致护肤品达不到最佳的效果，那么天气丹使用顺序图解是什么？天气丹用法步骤是什么呢？天气丹的套盒中产品是十分全面的，其中包括天气丹水
提起2020年飞天茅台与属相茅台区别，大家都知道，有人问茅台生肖酒的收 茅台飞天和五星的区别，另外，还有人想问飞天茅台0743和15635有什么区别我有一瓶2011年的飞天,第三排写着是15635,不是，你知道这是怎么回事？其实飞天茅台和
妮维雅男士水活多效洁面乳价格在37元左右，这款洁面乳的价格比较平民，不是太别贵。所以我们在购买的时候只需要根据自己的肌肤状态，选择控油、洁面或者清洁的洗面奶即可。其中妮维雅男士多效洁面乳，有均匀丰富的泡沫，味道很清新，密密麻麻的洁白泡沫，可
平价好用的护手霜在市面上很常见，品牌也是五花八门，相信很多集美都不知道该怎么挑选，作为一名多年的护肤达人，接下来我就分享给大家5款常用实惠好用的护手霜，快快收藏起来吧！凡士林护手霜参考价格：169元50ml凡士林护手霜的主要成分就是凡士林
