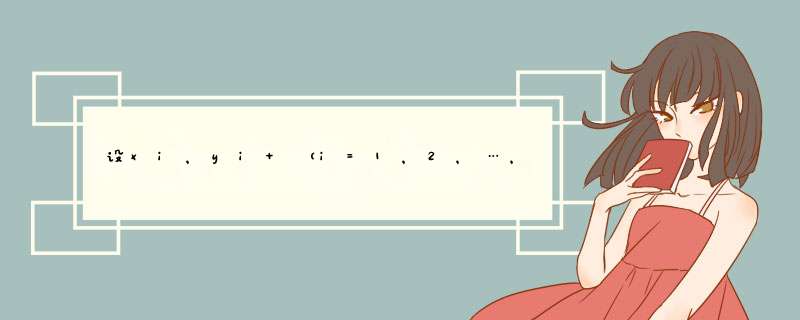
证明：要证
| n |
| i1 |
| n |
| i1 |
| n |
| i＝1 |
| n |
| i＝1 |
| n |
| i＝1 |
| n |
| i＝1 |
由于
| n |
| i＝1 |
| n |
| i＝1 |
| n |
| i＝1 |
| n |
| i＝1 |
而①的左边为乱序和，右边为顺序和，根据排序不等式可得①成立，
故要证的不等式成立．
MATLAB中”xy=[xi;yi];“的意思是，xi、yi的行向量数据（或列向量数据）以行矩阵或列矩阵的形式赋值给xy变量。例如：
1、xi、yi为行向量数据
>> xi=[1 2 3];yi=[3 4 5];
>> xy=[xi;yi]
xy =
1 2 3
3 4 5
2、xi、yi为列向量数据
>> xi=[1;2;3];yi=[3;4;5];
>> xy=[xi;yi]
xy =
1
2
3
3
4
5
matlab输入(xi，yi)，i=0…n步骤如下：
1、打开matlab软件并创建一个新的脚本文件(m文件)。
2、在脚本文件中输入代码(xi，yi)，i=0…n
3、运行代码，matlab将创建并存储xi和yi数组，可以在脚本中继续使用这些变量进行后续操作。
解答:解:由样本数据点集{(xi，yi)|i=1，2，…，n}求得的回归直线方程为
∧
y
=123x+008，且
x
=4
y
=123×4+008=5，
去掉两个数据点(41，57)和(39，43)，
x
=4
y
=5，
重新求得的回归直线ℓ的斜率估计值为12，回归直线方程设为:
∧
y
=12x+a，代入(4，5)，∴a=02
∴回归直线ℓ的方程为:
∧
y
=12x+02
故答案为:
∧
y
=12x+02
欢迎分享，转载请注明来源：品搜搜测评网
微信扫一扫
支付宝扫一扫
