用高斯求和法计算1+2+3+4+5+6.+（n-2)+(n-1)+n 要过程

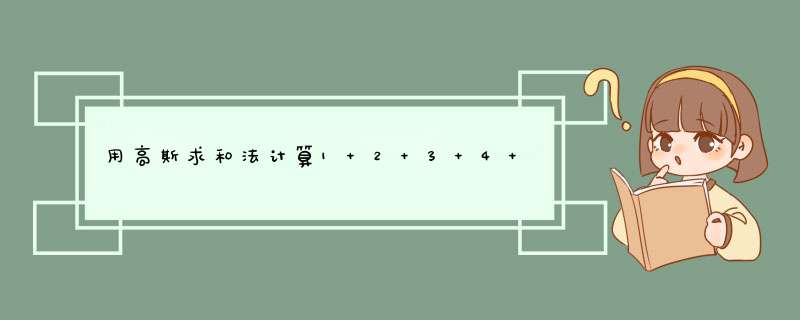
(1+n) n/2

适用于等差数列 ：

(首项+末项)项数/2=数列和

例题：1+2+3+4+5……+99+100

1就是首项,100就是末项,一共有100个项数

1+2+3++100

=(1+100)100/2

=101100/2

=10100/2

=5050

另外：末项＝首项+（项数-1）公差

项数＝（末项－首项）/公差+1

首项＝末项－（项数-1）公差

聪明的小高斯算的是高斯算平均数。

高斯算平均数是指将一组数据按照一定的算法进行处理，得到的平均值。这个算法的特点是对于异常值有较好的鲁棒性，可以排除极端值对结果的影响。小高斯可以通过这种算法来得到一组数据的平均值，同时可以排除掉可能存在的异常值，从而得到更加准确的结果。

具体的实际解答方式如下：首先，将一组数据从小到大排序，去掉最大值和最小值，然后对剩余的数据求平均值。这样得到的结果就是高斯算平均数。

当需要对一组数据进行平均值计算时，如果存在一些异常值，那么常规的算法可能会受到这些异常值的干扰，从而导致计算结果不准确。而高斯算平均数则可以排除掉这些异常值，得到更加准确的结果。因此，在实际应用中，高斯算平均数被广泛应用于数据处理和统计分析领域。

需要注意的是，高斯算平均数并不是万能的。在某些特殊情况下，它可能会失效，导致结果不准确。因此，在具体应用中，需要根据数据的特点和实际情况选择合适的算法。

法一：高斯求和法

设S1=1+2+3++100

   S2=100+99+98++1

则S1+S2=100101=10100

则S1=10100/2=5050

即1+2+3++100=5050

法二：中心数求和法

1至100中心数为505，

505乘以项数100，得5050

法三：梯形求和法（前提是公差为一）

构建一个梯形，上底（首项）为1，下底（末项）为100，高（项数）为100，

则此梯形面积（即1+2+3+4++98+99+100的结果）为（1+100）100/2

法四：分组求和法

    1+2+3+4++98+99+100

=（1+99）+（2+98）+（3+97）+······+（49+51）+50+100

=49×100+50+100

=5050

拓：

你可以用C++代码编辑器，粘贴以下代码并运行

#include<bits/stdc++h> 

int main()

 { 

 int i,sum=0; 

 for(i=1;i<=100;i++) 

 { 

 sum=sum+i; 

 } 

 printf("1+2+3+4++98+99+100结果为：%d",sum); 

return 0;

 }

望采纳

按照自然顺序相加 虽然可行 但是很繁琐 高斯发现 1 2100这100个数中,1+100=101,2+99=101,以此类推,就把一个没有丝毫规律的加法 变成了50个相同的数字相加,把加法转化为乘法,改变的运算方式,所以能很快的完成