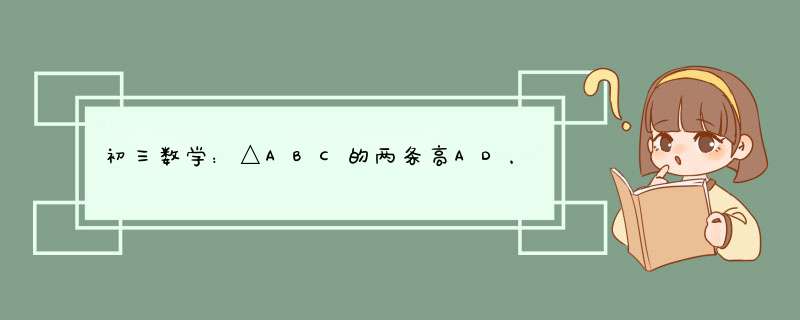
解:由已知条件可知在△BEF和△ADC中∠C为共用角
∴∠EBC=∠DAC
又∵DH=CD
∴RT△BDH≌RT△ADC
∴BD=AD
∴∠ABC=∠BAD=45°
等腰△ABC中,顶角∠A=36°,易得∠B=∠C=72°
F,G,D分别为AB,AC,BC中点,易得:
FG=BC/2,BD=CD=BC/2,DF‖AC,DG‖AB
∴FG=BC=CD ①
∠BFD=∠CGD=∠A=36°,∠BDF=∠CDG=∠B=∠C=72°
在圆O中,BC且圆O于D,由弦切角定理可得:
∠BDE=∠EFD=36°,∠CDH=∠HGD=36°
∴∠EDF=∠BDF-∠BDE=36°,∠GDH=∠CDG-∠CDH=36°
∴∠EFD=∠EDF,∠DGH=∠GDH
△EFD,△DHG都是等腰三角形
∴EF=DE,DH=GH ②
在△BDE中,由两内角∠B=72°,∠BDE=36°,易求出∠BED=72°
∴∠BED=∠B,△BDE是等腰三角形,有BD=DE ③
同理,可求出∠DHC=∠C=72°,△CDH为等腰三角形,有CD=DH ④
结合①,②,③,④,可得:
FG=DE=EF=DH=GH
∴五边形DEFGH为正五边形
解:
BD垂直于AC,CE垂直于AB,角A=60度所以∠DCH=90-60=30度,利用直角三角形中30度所对的边是斜边的一半可知HC=2HD=4,那么EC=HC+EH=4+1=5同理可得
BD=BH+HD=2EH+HD=2+2=4
角ACB=45度,那么△BDC是等腰直角三角形,BD=DCS△BDC=1/2BDDC=8
角A=60度,则DB=AD√3AD=DB√3/3=4√3/3S△ADB=1/2ADBD=8√3/3
三角形ABC的面积=S△BDC+S△ADB=8+8√3/3
附带说明一下,角A=60度,则DB=AD√3直角三角形ABD中,角ABD=30度所以
AD=1/2AB利用勾股定理,AB^2=AD^2+DB^2可得DB=AD√3
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
