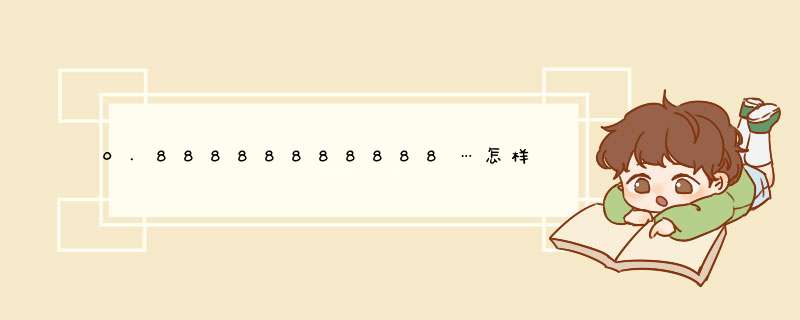
如果是纯循环小数,即小数点后直接开始循环的。如088888,0142857142857……等。0888……=8/9,0142857142857……=142857/999999=1/7 看出规律了么,就是循环部分除以循环部分位数个9,假如循环部分有五位,就除以99999。推导如下:为了方便叙述,假设循环部分有5位abcde,x=0abcdeabcde……①则(10^5=)100000x=abcdeabcdeabcde…② ②-①得99999x=abcde③ 所以x=0abcdeabcde……=abcde/99999 其他同理
025化成分数是四分之一。
025=25/100=1/4
小数化分数,小数点前不变,小数点后面有N位分子就乘以10的N次方,分母为10的N次方,然后约分化简例如15,就是1不变,05乘以10得5,分母为10,化简后就是3/2,其次要记住一些常量例如025=1/4、0125=1/8、05=1/2、02=1/5、033…3=1/3等等。
扩展资料:
一、无限循环小数化分数
无限小数又分无限循环小数和无限不循环小数,无限循环小数可以化成分数,而无限不循环小数属于无理数,无法化成分数无限循环小数又分纯无限循环小数(就是说,从十分位开始就是循环节,如012341234,其中1234为循环节)和混无限循环小数(就是说,十分位还不是循环节,如012333333,3为循环节)。
注:在这里,整数部分忽略不记,但在实际运算中必须加上;还有就是纯无限循环小数&混无限循环小数,这里“纯”和“混”是加上去的,可能这种说法不正确,所以不要随便说,但理解就好先说纯无限循环小数,化成分数,分子就是循环节。
而分母,就是循环节是N位,那分母就是N个9(这里是说99999这样连起来的自然数),如012341234,1234循环,循环节个数为4,那化成分数,就是分母为4个9,分子为循环节1234,即1234/9999再说混无限循环小数,化成分数。
分子就是小数点后面的非循环节部分和一个循环节连起来的数减去非循环节部分,分母是循环节位数个9和非循环节位数个0连起来,如012333333,3循环,分子就是123-12=111,分母是900,即111/900。
二、约分方法
方法一:可以用分子和分母的公因数(1除外)去除
例:
则
就是最简分数
像这样,把一个分数化成和它相等,但分子和分母都比较小的分数叫做约分(一般要化成最简分数)
方法二:直接用分数的分子和分母的最大公因数(1除外)去除
例:
则
就是最简分数
小结: 一般用分子和分母的公因数(1除外)去除分数的分子和分母,通常要除到最简分数为止。
-约分
-化分数
02化为分数是:五分之一。
解析:首先将02化成分母为10的分数,然后找出公约数进行约分即可。
02
=2/10(化成分母为10的分数)
=(2÷2)/(10÷2)(用公约数2进行约分)
=1/5
扩展资料:
分数化小数:
(1)分数化为纯循环小数。一个最简分数能化为纯循环小数的充分必要条件是分母的质因数里没有2和5,其循环节的位数等于能被该最简分数的分母整除的最小的99…9形式的数中9的个数。
(2)分数化为混循环小数。一个最简分数能化为混循环小数的充分必要条件是分母既含有质因数2或5,又含有2和5以外的质因数。
化成的混循环小数中,不循环的位数等于分母里的因素2或5的指数中较大的一个;循环节的位数,等于能被分母中异于2,5的因子整除的最小的99…9形式的数中,数9的个数。
用指定的分母做分母,整数乘以分母做分子。
如:把5化成分母为4的假分数,就用4做分母,5×4=20做分子,5=20/4。
所有的整数(0除外)都可以看成分母为“1”的假分数,可以根据需要依据分数的基本性质改变分子和分母的大小。
带分数要用整数×分母+分子做分子,分母不变的方式化成假分数。
扩展资料:
分母不是特殊数字的
1、利用分数与除法的关系:分子/分母=小数
2、如结果是循环小数,要根据实际情况保留几位小数就几位小数。
小数化分数
有限小数化分数,小数部分有几个零就有几位分母。如是纯循环小数,循环节有几位,分母就有几个9。
如是混循环小数,循环节有几位,分母就有几个9;不循环的数字有几位,9后面就有几个0,分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差。
例:012(2循环)=(12-1)/90=11/90
注意:最后结果不是最简分数就要约分。
—分数
欢迎分享,转载请注明来源:品搜搜测评网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
